La intuición nos puede engañar, las matemáticas no

Un conocido problema matemático sobre probabilidad es el de Monty Hall, inspirado en el concurso televisivo estadounidense Let’s Make a Deal. En el concurso, el presentador muestra tres puertas. En una de ellas puede haber un coche como premio; en las otras dos: una cabra.

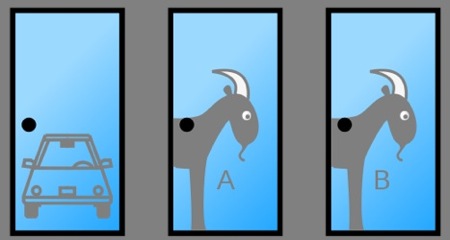
El concursante elige al inicio una de las puertas. A continuación, el presentador decide abrir otra de las puertas para mostrarle que tras ella, se esconde una cabra. Es entonces cuando se da la opción al concursante de quedarse con la puerta que había elegido inicialmente, o por lo contrario, cambiar de puerta.

Si tras la elección del concursante, el presentador muestra que en una de las puertas (supongamos C) hay una cabra, en las otras dos (A y B) están la cabra y el coche. No sabemos si la cabra en A y el coche en B, o si la cabra en B y el coche en A. En cualquier caso, quedan dos puertas, por lo que podemos pensar que la probabilidad de ganar el coche es del 50%. Da igual si el concursante se queda con la puerta elegida inicialmente o si decide cambiar de puerta. ¿O no…?

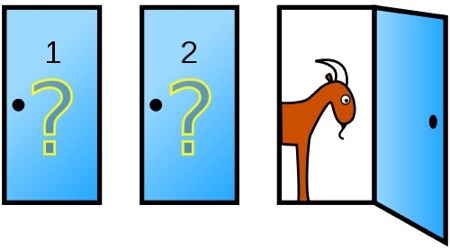
Bien, esto sólo es lo que nos dice la intución, que en esta ocasión nos engaña. De hecho, si el concursante cambia de puerta, matemáticamente las probabilidades de ganar son del 66%.

La explicación es la siguiente:

Si el concursante decide quedarse con la puerta elegida inicialmente, la probabilidad de haber acertado es de 1 sobre 3, es decir, de un 33%. No importa el hecho de que el presentador haya mostrado que en una de las puertas hay una cabra. El concursante ha decidido quedarse con su primera elección, y eso es en cualquier caso sigue siendo una opción entre tres posibles.

Sin embargo, si el concursante decide cambiar de puerta, puede haber 3 situaciones:

– Primer caso. El concursante había elegido la puerta que escondía el coche, y sin embargo, el cambiar, elegirá necesariamente la segunda de las cabras que queda por descubrir (la primera la mostró el presentador).

– Segundo caso. El concursante había elegido la puerta que esconde la primera cabra, por lo que al cambiar elige con total seguridad la puerta que esconde el coche (no olvidemos que antes de cambiar el presentador muestra una puerta con una cabra).

– Tercer caso. El concursante había elegido la puerta que esconde la segunda cabra, por lo que al cambiar elige como en segundo caso y con total seguridad la puerta que esconde el coche (no olvidemos que antes de cambiar el presentador muestra una puerta con una cabra).

De los 3 casos, uno supone perder y dos ganar, por lo que la probabilidad de ganar si cambiamos de puerta es del 66% (2/3), el doble que si el concursante decide no cambiar de puerta.

Si la explicación argumentada por escrito todavía no resuelve tus dudas, quizá esta escena de la serie Numbers te ayude a entender el problema.