Arte y matemáticas: números escondidos en el Partenón, la Mona Lisa y la manzana de Apple

Contaba no hace mucho cómo las matemáticas están presentes en la naturaleza, mucho más de lo que imaginamos. Formas, patrones, proporciones; infinidad de elementos surgidos de forma completamente natural que siguen un orden matemático y que son verdaderas demostraciones de belleza.

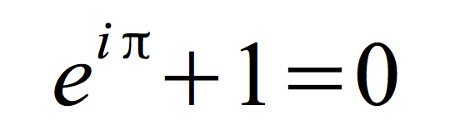
Siempre que se habla de belleza matemática aparece la famosa «identidad de Euler». Esta conocida fórmula del matemático más importante del siglo XVIII, está considerada la más bella de la historia por relacionar cinco números muy utilizados en la historia de las matemáticas y que además pertenecen a distintas ramas de la misma.

También las matemáticas estén presentes en diferentes expresiones artísticas. Podemos encontrar referencias matemáticas en muchas obras pictóricas y arquitectónicas. En este caso han sido los propios artistas los que desde hace siglos han considerado símbolo de belleza utilizar determinadas proporciones u organizar los elementos que componen la obra siguiendo un orden matemático. Este es el caso de obras como «La Mona Lisa» de Leonardo Da Vinci o «Las Meninas» de Velázquez. Ambas obras esconden el «número áureo», también llamado «divina propoción». Pero incluso diseños más recientes como los utilizados por la empresa de informática Apple, utilizan también este «mágico» número, por ejemplo en las proporciones del logotipo de iCloud.

¿Por qué es tan especial el «número áureo»?

En 300 a.C., Euclides, el padre de la geometría, descubre una proporción divina que rige todas las cosas bellas: el número áureo, representado por la letra griega φ (fi), en honor al escultor griego Fidias, que utilizaba este valor estético en sus esculturas.

El número áureo es un número irracional.

1.61803398874989484820458683436563811772030917980576286 2135448622705260462818902449707207204189391137484754088 0753868917521266338622235369317931800607667263544333890 8659593958290563832266131992829026788067520…

¿Cómo se puede obtener el número de oro?

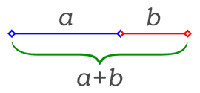El número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b que cumplen una determinada relación: la longitud total a+b es al segmento más largo a como a es al segmento más corto b.

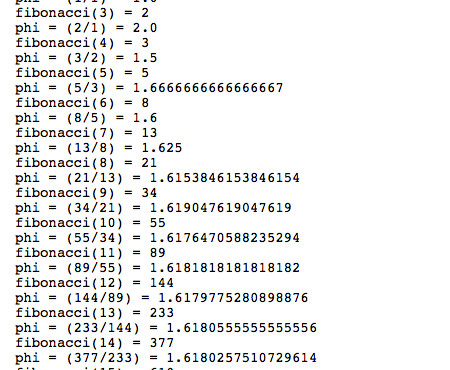
Aunque probablemente, la forma más curiosa de hallar una aproximación del mágico número áureo es a partir de la sucesión de Fibonacci (de la que ya hablé en el artículo «Huracanes, conejos y piñas: matemáticas en la naturaleza y cómo calcular la sucesión de Fibonacci»). Se trataría de realizar una sencilla operación sobre pares de número consecutivos en la sucesión de Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17111, 28657, 46638, … Por ejemplo, utilizando el siguiente programa en lenguaje Java genera los números de la sucesión de Fibonacci:

vamos calculando también en casa paso el cociente entre un valor y el anterior (3/2, 5/3, 8/5, 13/8, 21/13, …). Observaremos que el valor de la división se va aproximando cada vez más al número áureo: 1.61803398874989484820458…

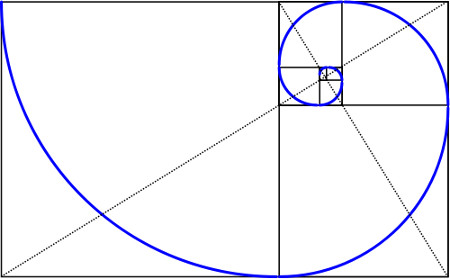
A partir de la evolución de un rectángulo dorado, que posee una proporcionalidad entre sus lados igual a la razón aúrea, podemos construir una espiral áurea, como las que aparecen «escondidas» en muchas obras de arte.

El número áureo en la arquitectura

El número áureo está presente en el diseño de la construcción del Partenón de Atenas. Si tomamos algunas medidas, podremos comprobar que la base frontal es la altura multiplicada por el número áureo (1,61803398). Y si estudiamos otros elementos de la construcción, la divina proporción vuelve a aparecer.

El número áureo en la pintura

En una de las obras de de Leonardo Da Vinci podemos encontrar una espiral áurea, delimitando las proporciones de «La Mona Lisa».

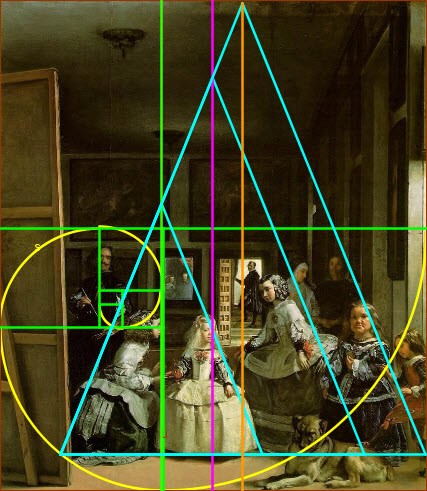
También en la famosa obra de Velázquez, «Las Meninas», aparecen varias referencias matemáticas, como por ejemplo los tres triángulos isósceles que marcan la posición de «las meninas», y también la espiral dorada.

La presencia de la espiral tiene una clara intención dentro del cuadro del pintor español:

Velázquez, en la composición áurea de su cuadro Las Meninas, lo ordena con la mencionada espiral, cuyo centro está situado sobre el pecho de la infanta Margarita, marcando con ello el centro visual de máximo interés y el significado simbólico del lugar reservado para los escogidos, como era tradición en Europa, que el monarca ocupara el lugar central y de privilegio en las ceremonias. No hay que olvidar que en el momento de la creación de la pintura, la infanta Margarita era la persona más indicada como sucesora al trono, ya que Felipe IV no tenía en ese momento ningún hijo varón.

La divina proporción en diseños modernos

Como comenta el blog Fotomat sobre fotografía y matemáticas, el logotipo de iCloud de Apple utiliza las proporciones áureas también. Pero no queda ahí la obsesión de los de Apple por la perfección. Indagando un poco más sobre tema, podéis descubrir que la famosa manzana utiliza proporciones extraídas de la sucesión de Fibonacci. Increíble.

«Los números son bellos» del programa tres14

Para comprender mejor toda la relación entre arte y matemáticas, recomiendo este reportaje del programa tres14, «Los números son bellos», en el que entrevistan a cuatro matemáticos. A todos ellos se les plantea la siguiente pregunta: «¿Qué tienen en común arte y matemáticas?». Francisco Martín Casalderrey y Capi Corrales hablan sobre mirar el arte con ojos matemáticos, Fernando Corbalán, sobre la divina proporción y Sebastià Xambó y Antonio J. Durán, sobre el arte en las matemáticas, su poesía y su belleza.

Programa Java en rextester.com | Cálculo del número áureo
La2 de rtve.es | tres14 – Los números son bellos