Empieza en el blog la sección «Trocitos de código», una serie de artículos donde comparto ejemplos de programas escritos con algún lenguaje de programación y que resuelve algún problema concreto, especialmente de matemáticas. Esta semana, la simulación de millones de lanzamientos de una moneda.
Etiqueta: GeoGebra
Después de escribir varias entradas con recursos de geometría, creo que es momento de presentar en forma de resumen lo publicado hasta el momento. Pretendo con ello reunir todos los apuntes sobre geometría de figuras planas elaborados hasta ahora.
Con «Matemáticas interactivas con GeoGebra» presentaba en primer lugar este software educativo para matemáticas diseñado principalmente para ser utilizado en colegios y universidades. Es un procesador geométrico y algebraico con el que podemos realizar infinidad de construcciones con puntos, segmentos, rectas, funciones, etc. Con la entrada «Geometría y álgebra en tu bolsillo» comentaba la versión portable de este programa, para llevarlo siempre en nuestro pendrive.
Los primeros apuntes de Geometría 2D fueron en forma de presentación, publicados en «Recursos de geometría: el Teorema de Pitágoras». En el artículo comparto algunos recursos -apuntes y ejercicios- publicados en una wiki diseñada para ello
Ingeniero en Informática y profesor de Programación, Inteligencia Artificial y Robótica en Secundaria. Escribo en Ocho en punto sobre organización personal y tecnología. En Esfera TIC me centro en educación y TIC. Mi web personal es un cajón de sastre, pero en mi boletín, La ventana digital, pongo orden y resumo lo más destacado.
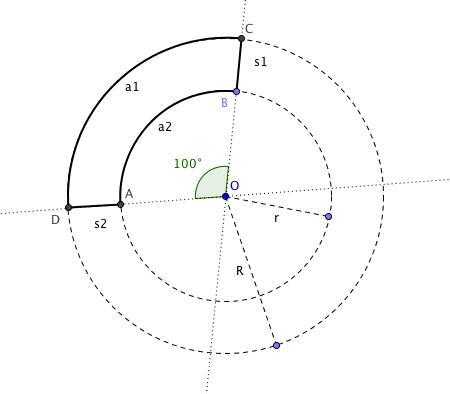
Traigo la segunda parte del tema de cálculo de áreas y perímetro de figuras planas, concretamente todas aquellas que involucran el número Pi en sus fórmulas.
Si esta semana te has propuesto resolver el desafío matemático de Los Arqueros, debes saber que la clave está en utilizar alguna de las fórmulas que presento hoy.
En la primera entrega publicaba una presentación resumiendo el cálculo de áreas como el rombo, trapecio, romboide, rectángulo, etc. y compartía en una wiki todas las figuras diseñadas con GeoGebra (archivos .ggb). Publico esta segunda parte utilizando el mismo formato y compartiendo todo el material
Ingeniero en Informática y profesor de Programación, Inteligencia Artificial y Robótica en Secundaria. Escribo en Ocho en punto sobre organización personal y tecnología. En Esfera TIC me centro en educación y TIC. Mi web personal es un cajón de sastre, pero en mi boletín, La ventana digital, pongo orden y resumo lo más destacado.
La geometría es probablemente la parte de las matemáticas donde más fácil resulta aplicar las TIC, sobre todo porque podemos verlas bien en 2 o 3 dimensiones. Es quizá por este motivo que incluso comprobar soluciones a problemas matemátios puede resultar hasta entretenido.
Ya he hablado en este blog sobre GeoGebra, un software educativo para el área de matemáticas, diseñado para trabajar con álgebra y geometría. Podemos utilizarlo para muchos propósitos, entre ellos, como digo, plantear algunos ejercicios de geometría para comprobar el resultado y de paso comprender aún mejor el desarrollo de la solución al problema. Ver el problema siempre ayuda.
Con esta entrada sobre geometría estreno sección de recursos en este blog. Antes de empezar el curso, dediqué varias entradas a aspectos de organización personal. Sin embargo, comentaba en la presentación de este blog que utilizaría también esta plataforma para compartir algunos de los materiales educativos que preparo o que voy descubriendo en otros blogs. Empezamos con algunos de geometría.
Esta mañana me ha llegado un enlace a una sección de la web de GeoGebra donde descargar una aplicación portátil de GeoGebra. Existen versiones de este programa portátil (en otros sitios traducido como aplicación portable) para Windows, Mac y Linux. Así que si quieres llevar tu GeoGebra siempre contigo a clase, ya puedes descargarlo y guardarlo en tu lápiz USB.
GeoGebra es un software educativo para matemáticas diseñado principalmente para ser utilizado en colegios y universidades. Es básicamente un procesador geométrico y algebraico con el que podemos realizar infinidad de construcciones con puntos, segmentos, líneas, cónicas, etc., simplemente utilizando el ratón y el teclado. En 2009 recibió la Distinción en Tecnología en los Tech Awards.