Comparto esta semana un ejercicio que consiste en transformar fórmulas de áreas de figuras planas de lenguaje matemático a lenguaje informático, utilizando la sintaxis de fórmulas de la hoja de cálculo. La actividad permite también revisar conceptos como el uso de los paréntesis o las reglas de precedencia de operadores.
Etiqueta: geometría
«El pastel de la abuela» es el tercer enigma del Concurso de Desafíos Matemáticos.
Los contenidos del blog que estás leyendo ahora mismo se publican bajo una licencia libre, concretamente Creative Commons BY-NC-SA 3.0. Esto quiere decir que cualquiera…
En el álgebra elemental, una expresión puede contener números, variables y operaciones aritméticas, y es fundamental saber transformar estas expresiones para aprender a descubrir nuevas fórmulas.
¿De dónde proceden los números f/ de las cámaras de fotos? ¿por qué exactamente siguen la sucesión 1, 1.4, 2, 2.8, 4, 5.6 y no otra? La explicación, lógicamente, es matemática.
Publico en esta entrada la séptima y última de las pruebas del concurso de desafíos matemáticos.
Y con El Quinto Elemento llegamos al penúltimo de los problemas de la I Edición del Concurso de Desafíos Matemáticos. Uno de los enigmas típicos son los de secuencias o progresiones, en las que hay que realizar algún cálculo sobre el elemento anterior para obtener el siguiente, o en las que hay que observar las posiciones de letras y números en cada elemento para intentar deducir el siguiente. En esta ocasión se trata de una secuencia de letras y números que hay que intentar continuar.
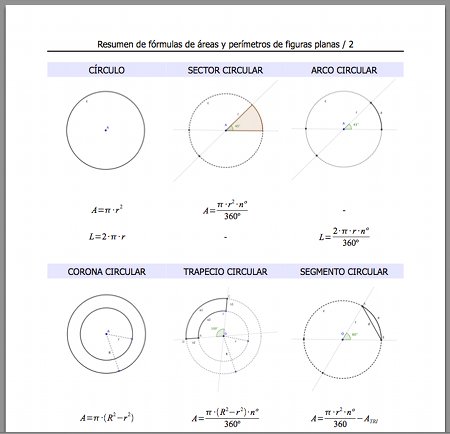
No quería terminar la semana sin antes dejar este documento en forma de chuleta de fórmulas de geometría 2D. Ayer presentaba un resumen de todo lo publicado hasta el momento sobre áreas y perímetros de figuras planas. Con este último documento cierro la primera serie de recursos sobre el tema.
Dejo también el enlace a la colección de documentos en Issuu
Ingeniero en Informática y profesor de Programación, Inteligencia Artificial y Robótica en Secundaria. Escribo en Ocho en punto sobre organización personal y tecnología. En Esfera TIC me centro en educación y TIC. Mi web personal es un cajón de sastre, pero en mi boletín, La ventana digital, pongo orden y resumo lo más destacado.
Después de escribir varias entradas con recursos de geometría, creo que es momento de presentar en forma de resumen lo publicado hasta el momento. Pretendo con ello reunir todos los apuntes sobre geometría de figuras planas elaborados hasta ahora.
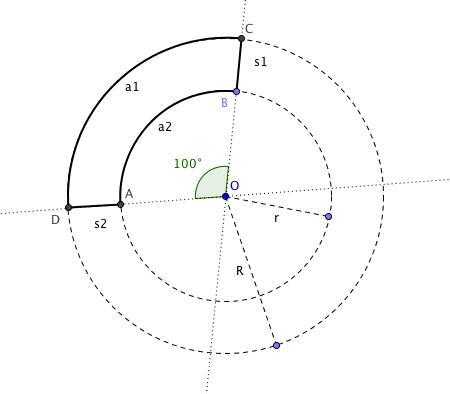
Con «Matemáticas interactivas con GeoGebra» presentaba en primer lugar este software educativo para matemáticas diseñado principalmente para ser utilizado en colegios y universidades. Es un procesador geométrico y algebraico con el que podemos realizar infinidad de construcciones con puntos, segmentos, rectas, funciones, etc. Con la entrada «Geometría y álgebra en tu bolsillo» comentaba la versión portable de este programa, para llevarlo siempre en nuestro pendrive.
Los primeros apuntes de Geometría 2D fueron en forma de presentación, publicados en «Recursos de geometría: el Teorema de Pitágoras». En el artículo comparto algunos recursos -apuntes y ejercicios- publicados en una wiki diseñada para ello
Ingeniero en Informática y profesor de Programación, Inteligencia Artificial y Robótica en Secundaria. Escribo en Ocho en punto sobre organización personal y tecnología. En Esfera TIC me centro en educación y TIC. Mi web personal es un cajón de sastre, pero en mi boletín, La ventana digital, pongo orden y resumo lo más destacado.
Traigo la segunda parte del tema de cálculo de áreas y perímetro de figuras planas, concretamente todas aquellas que involucran el número Pi en sus fórmulas.
Si esta semana te has propuesto resolver el desafío matemático de Los Arqueros, debes saber que la clave está en utilizar alguna de las fórmulas que presento hoy.
En la primera entrega publicaba una presentación resumiendo el cálculo de áreas como el rombo, trapecio, romboide, rectángulo, etc. y compartía en una wiki todas las figuras diseñadas con GeoGebra (archivos .ggb). Publico esta segunda parte utilizando el mismo formato y compartiendo todo el material
Ingeniero en Informática y profesor de Programación, Inteligencia Artificial y Robótica en Secundaria. Escribo en Ocho en punto sobre organización personal y tecnología. En Esfera TIC me centro en educación y TIC. Mi web personal es un cajón de sastre, pero en mi boletín, La ventana digital, pongo orden y resumo lo más destacado.