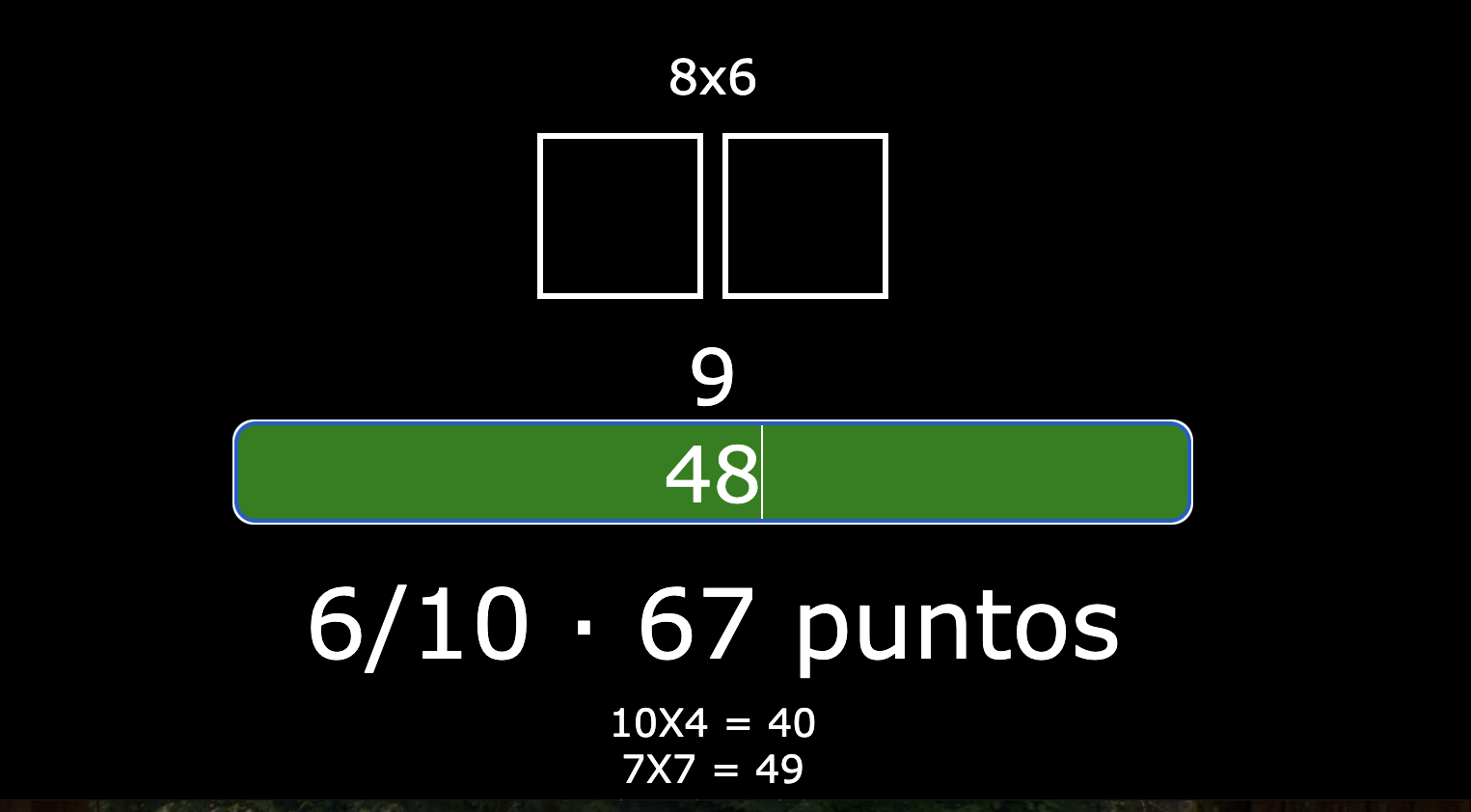
He adaptado el juego Shuffled, creado originalmente para trabajar con letras, para repasar las tablas de multiplicar de forma lúdica y digital. Hay dos versiones: una numérica, en la que los jugadores escriben el resultado de operaciones sin pistas; y otra con letras desordenadas, en la que deben formar el resultado en palabras, con alguna ayuda ocasional. Ambas fomentan el cálculo mental, la lógica, la atención y la gestión del tiempo. Esta propuesta demuestra cómo, con pequeños cambios, la tecnología puede ponerse al servicio del aprendizaje y adaptarse a distintos contenidos y competencias del aula.
Etiqueta: números
La informática son unos y ceros. Esta es la frase que repiten una y otra vez quienes intentan (no siempre con éxito) explicar el funcionamiento interno de cualquier dispositivo electrónico digital. Comparto en este artículo un par de vídeos que utilizo en el aula para explicar el proceso de conversión de binario y decimal. y viceversa.
Formas, patrones, proporciones; infinidad de elementos surgidos de forma completamente natural que siguen un orden matemático y que son verdaderas demostraciones de belleza. También las matemáticas estén presentes en diferentes expresiones artísticas. Podemos encontrar referencias matemáticas en muchas obras pictóricas y arquitectónicas.
Publico en esta entrada la séptima y última de las pruebas del concurso de desafíos matemáticos.
Esta semana propongo un segundo desafío matemático. Tras leer el enunciado puede parecer sencillo encontrar una solución al problema, sin embargo, seguro que os lleva…