 He programado esta aplicación web para facilitar el trabajo de redacción de observaciones e informes sobre el rendimiento académico de los alumnos. Se trata solo de un asistente que puede servir de guía o plantilla para no pasar por alto ningún aspecto relevante que convenga incluir en una observación académica.
He programado esta aplicación web para facilitar el trabajo de redacción de observaciones e informes sobre el rendimiento académico de los alumnos. Se trata solo de un asistente que puede servir de guía o plantilla para no pasar por alto ningún aspecto relevante que convenga incluir en una observación académica.
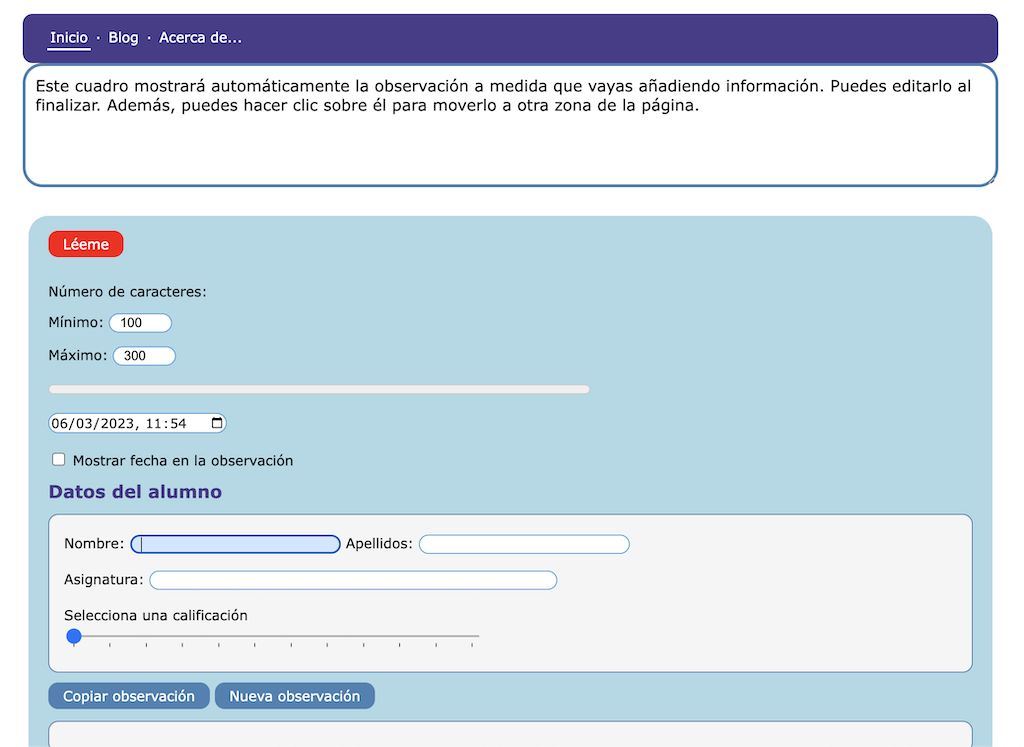
La aplicación web es gratuita y no almacena ninguna información que el usuario marca o introduce; tampoco el texto que genera. Aunque podemos generar un texto muy completo simplemente marcando algunas opciones, es importante escribir también en los campos disponibles para personalizar el texto de la observación. El informe debe ser personal e individualizado y la mejor forma es escribir nosotros mismos aquello que queremos destacar y aconsejar.
Ingeniero en Informática y profesor de Programación, Inteligencia Artificial y Robótica en Secundaria. Escribo en Ocho en punto sobre organización personal y tecnología. En Esfera TIC, sobre educación y TIC. Mi web personal es un cajón de sastre, pero en mi boletín, La ventana digital, intento poner orden. En ocasiones, escribo notas al vuelo.
