El álgebra elemental es la forma más básica del álgebra. A diferencia de la aritmética, en donde sólo se usan los números y sus operaciones aritméticas (como +, −, ×, ÷), en álgebra los números son representados por símbolos (usualmente a, b, c, x, y, z).
A estos símbolos los llamamos variables. En el álgebra elemental, una expresión puede contener números, variables y operaciones aritméticas, y es fundamental saber transformar estas expresiones para aprender a descubrir nuevas fórmulas.
Por ejemplo, para calcular la hipotenusa o alguno de los catetos de un triángulo rectángulo, no necesitamos memorizar cada una de las fórmulas (o no deberíamos), sino que partimos del Teorema de Pitágoras, para obtener las otras tres expresiones. Y utilizaremos cada una de ellas dependiendo de los datos que tengamos.
En un problema de áreas, no siempre se pide calcular el área de la figura para aplicar la fórmula directamente. Por ejemplo, para un triángulo, podrían darnos el valor del área y altura, para poder calcular su base. De estar forma, es posible transformar la fórmula original en una nueva.
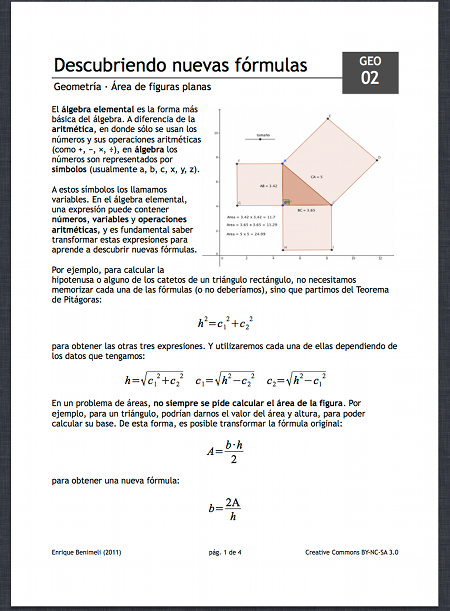
Sobre este tema, dejo publicado (bajo licencia Creative Commons) un documento de 4 páginas con ejemplos de transformaciones de algunas fórmulas de geometría de áreas planas.
Documentos | Descubriendo fórmulas (PDF, 4 páginas) | publicado en Issuu
Imagen | Math Wall de João Trindade en Flickr

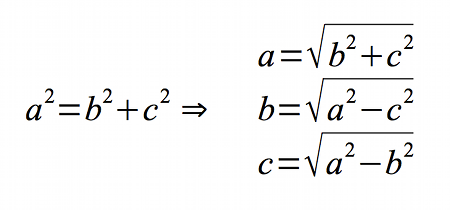
3 Comments
Ah el álgebra, que materia tan interesante, desde siempre me agrado, quizá por el hecho de que se me facilita mucho.
[…] Descubriendo nuevas fórmulas […]
Magnifico artículo