De amig@s invisibles y cálculo de probabilidades

Lo que ha sucedido este año podría parecer imposible. Sin embargo, sólo es improbable. Organizamos cada año el juego del amigo invisible entre profesores y otros compañeros de nuestro colegio. Alrededor de 45 personas. Y por tercera vez consecutiva, he vuelto a sacar el mismo nombre de la cesta. ¿Qué probabilidad hay de que esto suceda?

Se trata de un típico problema de probabilidades y, buscando similitudes con un problema de lanzamiento de dados y con ayuda de las TIC (el buscador de respuesta Wolfram|Alpha),  podemos realizar el cálculo rápidamente.

Se organiza el juego del amigo invisible tres Navidades seguidas. Los tres eventos son, por tanto, independientes entre sí. Es decir, sacar un papel con un nombre de un cesta con otros 44 nombres, es un experimento aleatorio que no depende de lo que sucediera el año pasado. Son por tanto sucesos independientes. Hagamos primero un cálculo teórico:

Definiendo los 3 sucesos independientes:
A = «sacar X como amig@ invisible» (en 2009)
B = «sacar X como amig@ invisible» (en 2010)
C = «sacar X como amig@ invisible» (en 2011)

y suponiendo que en los tres experimentos participa el mismo número de personas, 45 (el número de asistentes es entre 40 y 50), la probabilidad de sacar el nombre X de la cesta es:

P(A) = P(B) = P(C) = 1/45

La probabilidad de la ocurrencia conjunta de los 3 sucesos, que llamaremos «probabiliad de triamigo» es:

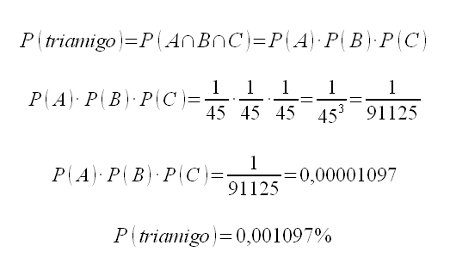El cálculo de probabilidades para el experimento del amigo invisible es exactamente el mismo que el de calcular la probabilidad de obtener 3 caras iguales (por ejemplo «6»)  lanzando 3 dados de 45 caras.

El lanzamiento de dados es un ejemplo clásico cuando uno empieza a estudiar los primeros conceptos de la teoría de probabilidades. Como no podría ser de otra forma, el buscador de respuestas Wolfram|Alpha cuenta con estas funciones de cálculo. Escribiríamos como términos de búsqueda:

3 sixes on 3 45-sided dice

(3 seises en 3 dados de 45 caras)

Observamos que el resultado es exactamente el mismo: existe una 1 posibilidad entre 91125 de que te toque 3 años seguidos el mismo amigo invisible. Y a mí me ha sucedido este año. Historia real.

Ejemplos Wolfram|Alpha | Ejemplos con lanzamiento de dados
Un caso práctico | Lanzamiento de 3 dados con 45 caras