Azar y probabilidad: la falacia del jugador

Algo tiene la probabilidad que, incluso tratándose de matemáticas, tiene cierto éxito entre otros temas del libro. Al menos al principio. También es cierto que cuando se introducen conceptos de teoría de conjuntos, combinatoria y otras formulaciones, muchas veces la emoción por el tema se desvanece. En cualquier caso, parece que todo lo que tenga que ver con el juego, siempre atrae más al alumnado.

La probabilidad estudia los experimentos aleatorios o de azar. El cálculo de probabilidades trata de medir hasta qué punto puede suceder un fenómeno. Y en ocasiones nos sorprendería la probabilidad teórica de un suceso, frente a lo que pueda decir nuestro instinto.

Presento en este artículo algunos ejemplos y recursos que pueden servir para motivar el tema de probabilidad en el aula.

Números «feos» en la lotería… ¿pero improbables?

En 1903 tocó el Gordo de Navidad con el número 20297, y 103 años después, en 2006, volvió a salir el mismo número. Ocurrió también en 1956 y 1978, con el número 15560. La pregunta es, ¿jugarías estas Navidades a la lotería con algún número que ya hubiera salido años anteriores? Un primer impulso sería «jugar mejor a otro número», argumentando que ya tocó, y además, en dos ocasiones cada uno. Y si el número hubiera sido uno como el 01010, probablemente tampoco jugaríamos, pero por otros motivos: parece poco probable.

Hay números que a primera vista parecen más probables, y de otros números diríamos que es imposible que salieran en un sorteo. Por otro lado, existe en muchos lugares la tradición de jugar al mismo número cada año (con la creencia de que así aumentan las probabilidades). Nada de esto es cierto. Pensar que los sucesos pasados afectan a los futuros en lo relativo a actividades aleatorias, como en muchos juegos de azar, es lo que se conoce como la falacia del jugador.

La falacia del jugador: cuando la intuición falla

El programa tres14 hablaba precisamente sobre el fenómeno, de cómo al jugar a la lotería, hay números que nos despiertan más confianza que otros. Por ejemplo, si tuviéramos que elegir entre jugar al 03333 o al 25687, una gran mayoría optaría por el segundo, cuando sabemos que uno u otro son igualmente probables.

La falacia del jugador puede comprender varias ideas equivocadas. La primera es que un suceso aleatorio tiene más probabilidad de ocurrir porque no ha ocurrido durante cierto periodo. Por ejemplo, si al lanzar una moneda 10 veces ha salido cara, quizá pensemos que es más probable que salga cruz en la siguiente tirada, cuando en realidad, en cada lanzamiento de moneda, sacar cara y cruz son sucesos equiprobables.

Otra razonamiento erróneo es que un suceso aleatorio tiene menos probabilidad de ocurrir si ocurrió recientemente. Volviendo al ejemplo de la lotería, podríamos pensar que si durante dos años consecutivos ha tocado el mismo número en nuestra ciudad, es muy improbable que vuelva a suceder. En realidad, podríamos decir cada año «se pone el contador a cero» en lo que a probabilidades se refiere. El hecho de que haya tocado la lotería el año pasado no influye en la probabilidad de que toque dicho número de nuevo en las Navidades de este año.

Otro ejemplo de falacia es un clásico chiste de matemáticos, que dice así:

Cuando vuela en avión, un hombre decide llevar siempre una bomba consigo. «Las probabilidades de que en un avión haya una bomba son muy pequeñas —razona—, ¡así que las probabilidades de que haya dos son casi nulas!»

Seguramente nosotros no haríamos nunca un razonamiento como el del viajero en el avión, pero en otras situaciones sí podríamos dejarnos llevar por el instinto y equivocarnos en nuestra decisión (de realizar una apuesta, por ejemplo).

Sucesos aparentemente improbables

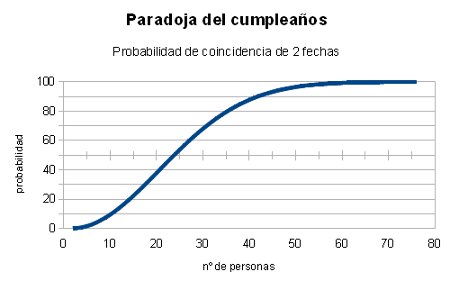
¿Apostarías algo a que en un grupo de 23 personas al menos 2 cumplen años el mismo día? Seguramente la primera respuesta intuitiva es «no». Sin embargo, sabiendo que la probabilidad es de más del 50%, quizá valdría la pena arriesgar. Este problema se conoce como la paradoja del cumpleaños, que expliqué ya con un caso práctico, un experimento con grupos de contactos en una red social.

Otro ejemplo que demuestra que debemos fiarnos más de las matemáticas que de nuestro propio instinto es el conocido problema de Monty Hall. La explicación detallada de por qué la opción aparentemente menos probable tiene en realidad el doble de probabilidad, la publiqué en «La intuición nos puede engañar, las matemáticas no». Un buen resumen es esta escena de la serie Numbers:

Falacia del jugador | Wikipedia | Programa tres14: «Curiosidades científicas – Nuestra intuición falla con el azar»
Reportaje | Loterías, retando a la probabilidad
El problema de Monty Hall | La intuición nos puede engañar, las matemáticas no
La paradoja del cumpleaños | Experimento en redes sociales