Trocitos de código (II). Recursividad y la función factorial

Leí en el blog Fotomat sobre fotografía y matemáticas una fantástica frase para explicar la recursividad. También la fotografía que publica refleja perfectamente el concepto.

«Si un genio te ofrece tres deseos dile que te bastan dos: El 1º lo que quieras y el 2º otros dos deseos. Eso es recursividad.»

Una definición de recursividad (también llamada recursión o recurrencia) sería

«La recursividad es la forma en la cual se especifica un proceso basado en su propia definición.»

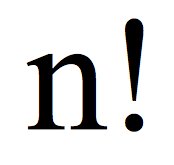
Como se puede observar en la imagen, en el cuadro que sostiene la chica, aparece de nuevo la imagen completa original. Y así sucesivamente, idealmente hasta el infinito. Sin embargo, cuando se utiliza la recursividad en matemáticas, es necesario definir lo que se denomina «caso base», una condición que permite evitar el carácter infinito de la recursividad.

Podemos encontrar muchos ejemplos de recursión en las funciones matemáticas. Uno de los ejemplos clásicos de funciones que pueden definirse de forma recursiva son la función factorial de un número: n!

¿Qué es el factorial de un número?

De nuevo, una definición:

Para todo entero positivo n, el factorial de n o n factorial se define como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta n.

La letra pi mayúscula que aparece en la fórmula se llama productorio, y es un operador matemático (como el sumatorio) que representa una multiplicación de una serie de números (finita o infinita).

Es decir, para calcular por ejemplo el factorial de 6, y se expresa como 6!, habría que realizar el producto de los número naturales desde 1 (k=1) hasta 6 (que es el valor de n).

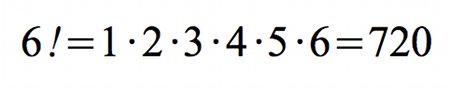
Se dice que este método para calcular la función factorial es de tipo iterativo. Se realiza un recorrido (iteración) por los distintos números, multiplicando en cada paso cada número de la serie por el siguiente (que es el anterior más 1).

Se trata de una función que aparece con mucha frecuencia en los cálculos de combinatoria (combinaciones, variaciones y permutaciones), fundamental para el cálculo de probabilidades. De hecho, en cualquier calculadora científica, podemos encontrar una tecla que realiza precisamente esta función sobre un número.

Pero también existe una definición recursiva de la función factorial.

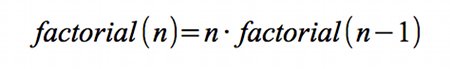
Podemos observar que en la definición de la función factorial (la expresión a la derecha del símbolo «=»), aparece de nuevo la función factorial. Esta situación corresponde con la definición de recursividad que comentábamos al principio: «la forma en la cual se especifica un proceso basado en su propia definición.»

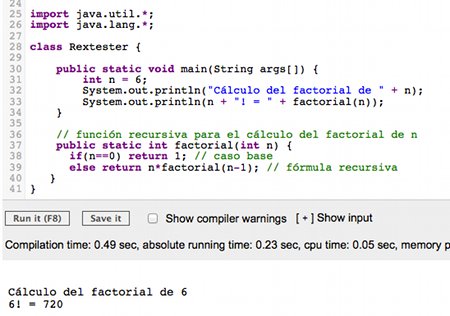
Ahora sabemos que la calculadoras disponen de la función factorial. Pero, ¿cómo se puede programar este cálculo con un ordenador? Los lenguajes de programación también permiten definir funciones de forma recursiva, y un ejemplo de implementación de la función factorial en Java sería la siguiente (clic sobre la imagen para probar el código).

El desarrollo de la función factorial de forma recursiva según el código anterior sería:

factorial(6) = 6·factorial(5)
factorial(5) = 5·factorial(4)
factorial(4) = 4·factorial(3)
factorial(3) = 3·factorial(2)
factorial(2) = 2·factorial(1)
factorial(1) = 1·factorial(0)
factorial(0) = 1

Y procediendo y resolviendo en orden inverso:

factorial(0) = 1
factorial(1) = 1·factorial(0) = 1
factorial(2) = 2·factorial(1) = 2·1 = 2
factorial(3) = 3·factorial(2) = 3·2 = 6
factorial(4) = 4·factorial(3) = 4·6 = 24
factorial(5) = 5·factorial(4) = 5·24 = 120
factorial(6) = 6·factorial(5) = 6·120 = 720

Este último paso se denomina caso base. En algún momento, la recursión debe terminar. Si ni impusiéramos una última condición, la recursión seguiría indefinidamente.

Código Java | Función factorial
En Tiching | Recursividad y la función factorial
Foto Recursividad | Fotomat
Foto Calculadora | por Simon Q en Flickr