5 vídeotutoriales y 12 ejercicios de estadística: cálculo de la media, la moda y la mediana

Imaginemos las siguientes situaciones. Toda ellas plantean una serie de cuestiones.

(1) Un grupo de alumnos de una clase de 3ºA de ESO realiza dos exámenes de historia durante el primer trimestre ¿cómo podemos «medir» el progreso general de la clase en el segundo examen respecto a los resultados del primero? ¿cómo podemos «comparar» los resultados con los del grupo B?

(2) Para la asignatura de Informática se propone a cada alumno la realización de un trabajo sobre un tema a elegir de una lista de ocho diferentes. Tras la elección de cada uno, ¿cuál el tema más popular entre los alumnos»

(3) Estudiamos la altura de los jugadores de un equipo de baloncesto. ¿Qué medida puedo utilizar para comparar la «altura del equipo» con la de otro?

Parámetros estadísticos

Para cada una de las preguntas planteadas anteriormente necesitamos un indicador, un parámetro, una medida, un punto de referencia para poder interpretar cómodamente los distintos grupos de datos y ofrecer una respuesta en forma numérica.

En particular, para este tipo de cuestiones, podemos calcular, según cada caso, tres parámetros de centralización diferentes: la media, la moda o la mediana. Son una herramienta que nos permite analizar mejor los datos, con el fin de comparar o tomar algún tipo de decisión.

Los siguientes vídeos pertenecen a Educatina, una biblioteca de vídeos educativos sobre una gran variedad de materias y disponible de forma gratuita en Internet. El primero de ellos es una introducción a los parámetros estadísticos.

Media aritmética

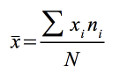La media aritmética, también llamada simplemente media o promedio, es el valor característico de una serie de datos y se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. El segundo vídeo explica cómo se realiza el cálculo de la media aritmética.

Mediana

La mediana representa el valor de la variable estadística de posición central en un conjunto de datos ordenados. El conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra. Es decir, la mediana deja a ambos lados el mismo número de datos. Si existen valores extremos, su cálculo no se ve afectado.

El tercer vídeo está dedicado a explicar el proceso de cálculo de la mediana.

Moda

La moda es un parámetro de centralización muy sencillo de calcular y que corresponde con el valor que tiene mayor frecuencia absoluta en una distribución de datos. Es decir, el valor que más se repite.

Una distribución es bimodal cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es aquella en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.

El cuarto vídeo presenta el cálculo de la moda en un grupo de datos.

Problema resuelto

El último vídeo de la biblioteca Educatina presenta un ejemplo completo de problema de estadística en el que se calculan los tres parámetros de centralización comentados anteriormente: la media, la moda y la mediana.

Un pediatra ha obtenido una tabla con los meses de edad a los que 50 niños empezaron a caminar. El objetivo es estudiar dicha tabla realizando los cálculos de media, moda y mediana.

Ejercicios de media, moda y mediana

A continuación comparto este documento con ejercicios de cálculo de parámetros de centralización.

Educatina.com | Biblioteca de vídeos educativos
5vídeos | Intro | Media | Moda | Mediana | Problema
Ejercicios (PDF, 2 páginas) | Media, moda y mediana
Fotografía | «statistics often lie» de mac steve en Flickr